1 Intevep. Construcción y Mantenimiento de Pozos.
Correo-e: [email protected]
2Universidad Central de Venezuela.
Comisión de Estudios de Postgrado - Facultad de Ingeniería.
Correo-e: [email protected]
La perforación direccional ha jugado un rol importante en el panorama energético mundial debido a que el desarrollo de pozos horizontales y de alcance extendido ha incrementado la producción de hidrocarburos en más del doble en los últimos años. Las fuerzas generadas entre la tubería de perforación o completación y las paredes del pozo, causadas por la fricción en el hoyo y comúnmente denominadas como torque y arrastre, son las responsables de limitar a la industria de la perforación a alcanzar mayores profundidades. Por otro lado, el centralizar correctamente la tubería dentro del hoyo es un factor clave que afecta de manera importante el flujo de fluidos en el pozo, la efectividad del proceso de remoción de lodo y el éxito de la cementación del anular. En este trabajo se presentan las bases teóricas que soportan un nuevo modelo tridimensional de fricción en el hoyo basado en elementos finitos, y fundamentado en un análisis numérico del modelo de Johansick (1983), para la estimación, a través de métodos iterativos, del torque y el arrastre durante la fase de completación del pozo y para el cálculo del standoff una vez colocado el tubular. Finalmente se muestra la aplicación del modelo en algunos casos de campo, obteniendo un excelente ajuste con datos reales, con errores medios absolutos menores al 3% en los casos analizados.
Palabras Clave: Torque y arrastre; Centralización; Completación; Elemento finito; Perforación direccional.
Directional drilling has played an important role in the world energy scene because the developments horizontal and extended reach wells have increased hydrocarbon production more than twice in recent years. The forces generated between the drill or completion pipe and the walls of the well, caused by friction in the hole and commonly called torque and drag, are responsible for limiting the drilling industry to reach greater depths. On the other hand, properly casing centralization is a key factor that greatly affects the flow of fluids into the well, the effectiveness of mud removal process and the cementing job success. This paper will describe the theoretical bases that support a new three-dimensional model of friction in the hole based on finite elements and fundamented on a Johansick model (1983) numerical analysis, for torque and drag estimations, through iterative methods, during the well completion and to calculate the standoff once placed the casing. Finally, the model application in field cases is shown, showing an excellent fit with real data, with absolute means errors less than 3% in the analyzed cases.
Keywords: Torque and drag, Centralization, Well completion, Finite element,Directional drilling.
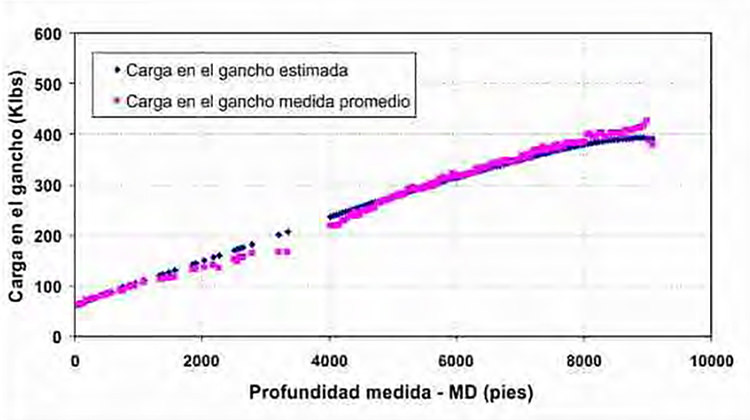
La tecnología en perforación ha avanzado rápidamente en los últimos 10 años. Tal y como se muestra en la Figura 1, la barrera de los 30.000 pies de alcance ha sido superada varias veces y diferentes operadoras están activamente planificando pozos entre 36.000 y 49.000 pies (Ghiselin, 2009). Desde que secciones de hoyos horizontales están siendo perforadas en longitudes que exceden los 20.000 pies de alcance, la ubicación de las herramientas de perforación y tuberías de completación a las profundidades planificadas podría no ser posible bajo ciertos planes de perforación. Esta situación puede ser especialmente crítica en hoyos horizontales. Durante los primeros años de construcción de pozos horizontales, el peso en el gancho usualmente era suficiente para empujar la tubería de completación hasta la profundidad total planificada. Con el inicio de la perforación de longitudes extremas adquiere importancia el modelado anticipado del plan de completación del pozo con la finalidad de determinar 1) si la tubería de completación puede soportar las deformaciones (tensión, compresión y torque) de instalación, y 2) si se tiene suficiente peso sobre el gancho para poder posicionar la tubería de completación a la profundidad total planificada. Debido al aumento de los costos y riesgos en estos escenarios, la capacidad de evaluar con precisión los diversos esfuerzos a los cuales va a estar sometida la tubería de completación durante su instalación pasa a ser una tarea fundamental para el éxito del pozo.
El análisis de las fuerzas presentes durante el proceso de perforación e instalación de tuberías de completación de pozos es una tarea imprescindible durante el diseño de la construcción de un pozo de alcance extendido, y el mismo se ha venido realizando durante los últimos 30 años haciendo uso de diferentes modelos analíticos presentados en la literatura. El método más comúnmente usado para este tipo de tareas es el modelo de torque y arrastre desarrollado originalmente por Dawson y Lane (Johancsik, 1983) y planteado en ecuaciones diferenciales por Sheppard (1987). Debido a la simplicidad y a la disponibilidad general de este modelo, ha sido usado extensivamente para la planificación y durante las operaciones en el campo. En términos más básicos, un modelo de sarta debe determinar la trayectoria de un tubo elástico confinado dentro de un hoyo. El tubo elástico puede establecer contacto con el hoyo en numerosos lugares en forma de un punto de contacto o contacto continuo, y el punto de contacto debe ser determinado por el proceso de cálculo. Además, las nolinealidades geométricas asociadas con la trayectoria del hoyo usualmente violan las consideraciones básicas usadas en el desarrollo de las ecuaciones propuestas en la bibliografía especializada, por lo cual se deben usar relaciones elásticas más generales (Love, 1944) (Nordgrem, 1974). Una de las formulaciones más conocidas es la desarrollada por Walker y Friedman (1977). Una publicación que a menudo se pasa por alto, es el trabajo de Ho (1986). Ho siguió este trabajo con una simplificación para modelos de tubería flexible (Ho, 1988). Ho también usó un sistema de coordenadas curvilíneas basadas en las ecuaciones de Serret-Frenet para una curva en el espacio. El modelo de torque y arrastre resuelve el problema de contacto con el hoyo pero suponiendo que la trayectoria de la sarta es la misma que la trayectoria del pozo. Además el contacto se supone continuo. Esta trayectoria está ciertamente dentro de una tolerancia de centímetros de la trayectoria de la sarta actual. Desafortunadamente, el modelo de cálculo de trayectoria más comúnmente usado (mínima curvatura) implica que los momentos flectores no son continuos en las estaciones de medición. La solución a este problema es suponer que la sarta es una viga con una simple fuerza, y la misma se asume tangente a la trayectoria del pozo. Debido a que la rigidez a la flexión es despreciada, el modelo de torque y arrastre es usualmente denominado como cable, cadena o tubería flexible. Note que esta consideración no es necesaria si se usa un modelo para determinar la trayectoria del pozo suficientemente lisa.
Se define el problema en su forma más general, sea pi el punto inicial donde comienza la perforación o el hoyo y pf el punto final, objetivo de la perforación. En principio para lograr ese objetivo de la perforación o la correcta completación se dispone de un ensamble recto, compuesto por una sucesión de tubos y aditamentos que pueden ser de sección variable. Apartando los cambios de dirección inducidos, la trayectoria ideal sería una línea recta; sin embargo, la litología del terreno y la dinámica del proceso de perforación inducen una distorsión a esta trayectoria. En síntesis, el problema consiste en analizar una viga que toma la forma de la trayectoria del pozo y sobre la cual actúan adicionalmente su propio peso y las solicitaciones de fuerza, torque y momento generados. Es obvio que, independientemente de las solicitaciones externas tipo fuerza (peso de la sarta), deben existir puntos de contacto entre la pared y la sarta; estos puntos son de importancia para la determinación de los esfuerzos y deformaciones, así como también para calcular el torque y el peso sobre el gancho (en pi). En este trabajo se establece como punto de partida la configuración deformada para la determinación de las cargas a las que va a estar sometida la tubería en fondo de pozo. La sarta en estas condiciones es sometida a la acción externa de su peso, e inicialmente esta configuración deformada está libre de esfuerzos y deformaciones, y los puntos de contacto serán considerados en nodos definidos.
Modelo teórico. El revestidor será modelado como una viga espacial. En términos del método de los elementos finitos (MEF), el sistema de revestimiento será discretizado como un conjunto de elementos de vigas con dos nodos. A cada nodo se le asocian las variables discretas que constituyen las incógnitas de nuestro problema.
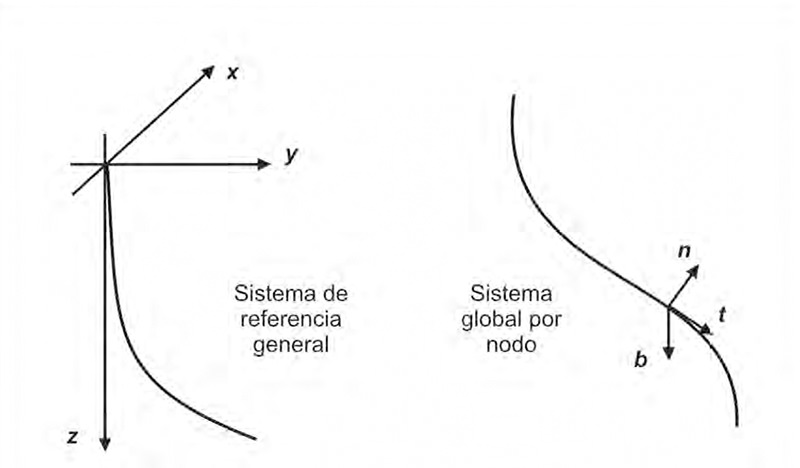
Sistema de referencia general. Se define el siguiente sistema de ejes cartesianos fijos, respecto al cual se refiere toda la geometría del problema, ver Figura 1. El origen se ubica en la superficie de la tierra, punto donde se inicia la perforación y donde comienza el pozo. Adicionalmente cumple con las siguientes condiciones:
Modelado de la trayectoria. Para el cálculo de la trayectoria de un pozo se utilizan un conjunto de datos, cada uno de los cuales consiste en mediciones de inclinación, azimut y profundidad. Para efectos de la construcción del modelo geométrico es necesario representar la trayectoria del pozo en coordenadas cartesianas (x, y, z). En este trabajo, los cálculos de trayectoria se realizarán aplicando el método de mínima curvatura debido a su precisión y el método tangencial en aquellas secciones de pozos en las cuales el método de mínima curvatura no sea aplicable.
Una vez definida una suficiente cantidad de puntos (x, y, z) a través del pozo, se debe proceder a representar dicha trayectoria como una curva continua y derivable en el dominio considerado. Dicha curva se construye por secciones a través del cálculo de un “spline” cúbico (polinomio de Lagrange). Es importante mencionar que estas ecuaciones fueron desarrolladas para el caso plano y el problema está definido en el espacio, es por ello que el cálculo de la trayectoria continua se debe definir en forma paramétrica, utilizando a una longitud de arco inicial (lo) como parámetro común, definiéndose éste como la suma acumulativa de las distancias entre nodos consecutivos. El cálculo del “spline” se realiza tres veces, una por cada dirección, resultando de esto las funciones definidas a trozos x( lo ), y( lo ) y z( lo ), y a partir de estas funciones definimos nuestra curva parametrizada de la forma r( lo ) = x(lo ), y(lo ), z( lo ) = x(lo)i+y(lo)j+z(lo)k, donde r representa nuestra trayectoria.
Sistema de ejes locales y globales Cada componente del sistema de revestimiento se discretiza en un conjunto de elementos finitos, cada elemento ocupa una longitud de arco dentro de la curva spline que define la trayectoria. El sistema de ejes globales de elementos finitos consiste en una terna definida en cada nodo de la malla: “t” será el vector tangente que sigue el sentido de la perforación, “n” será el vector normal que apunta al centro de la curvatura y “b” el vector binormal. Este sistema varía a lo largo de la trayectoria, y se le denomina comúnmente como sistema de coordenadas curvilíneas ortogonales. Los ejes globales serán denominados indistintamente según los vectores unitarios (t, n, b). El sistema local está constituido por el eje 
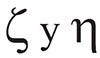
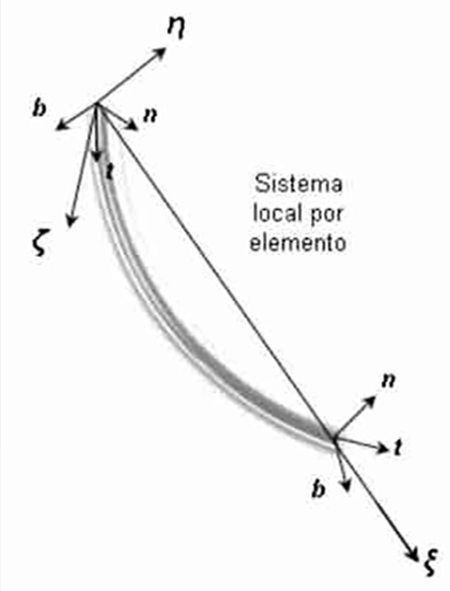
Como se ha venido mencionando el sistema de revestidores va a ser modelado a través de un conjunto de elementos de vigas espaciales. Un elemento de viga espacial es utilizado para modelar vigas rectas de sección transversal arbitraria, la cual puede deformarse no únicamente en la dirección axial sino también en la dirección perpendicular a su eje. La viga es capaz de soportar tanto fuerzas axiales y transversales, como momentos. De hecho, los elementos de viga pueden ser encontrados en muchos de los problemas de estructuras en el mundo real. El elemento general de viga a usar está compuesto por 2 nodos y seis grados de libertad por nodo: tres desplazamientos traslacionales en las direcciones 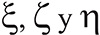
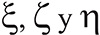

Donde Iy y Iz representan el segundo momento de área (o momento de inercia) de la sección transversal de la viga con respecto a los ejes Y y Z, respectivamente, y la longitud del elemento le=2a. Se asume que los nodos locales 1 y 2 del elemento corresponden a los nodos globales i y j, respectivamente. El desplazamiento en un nodo local debe tener tres componentes traslacionales en las direcciones X, Y y Z, y tres componentes rotacionales con respecto a los ejes X, Y y Z. Estos están numerados secuencialmente por d1 – d12 correspondientes a las deformaciones físicas. El desplazamiento en un nodo global debe también tener tres componentes traslacionales en las direcciones t, n y b, y tres componentes rotacionales con respecto a los ejes t, n y b de ese nodo. Estos se enumeran secuencialmente de la forma D6i−5, D6i−4 , . . . , y D6i. La transformación de coordenadas toma la relación entre el vector desplazamiento de basado en el sistema de coordenadas local y el vector desplazamiento De para el mismo elemento pero basado en el sistema de coordenadas global.
de = TDe (2)
Donde T es la matriz de transformación para un elemento viga, calculada a partir de las direcciones del sistema (t, n, b), y dada por:
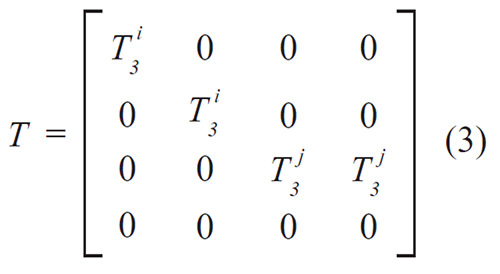
En la cual
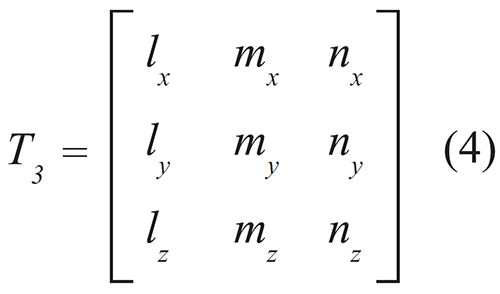
Donde lk , mk y nk (k = x, y, z) son los cosenos directores. Usando la matriz de transformación T, las matrices para un elemento viga espacial en el sistema de coordenadas globales pueden ser obtenidas de la forma:
Ke= T T ke T (5)
Fe = T T fe (6)
Donde fe es el vector fuerza del elemento en coordenadas locales, determinado de la forma:
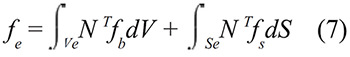
En terminología de un elemento finito orientado espacialmente, considerándolo recto, la dirección de la fuerza originada por el peso propio queda definida por el ángulo que forma el eje 
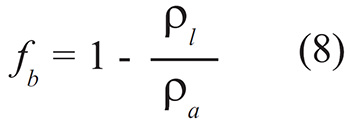
Donde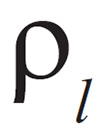
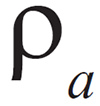
Una vez determinadas las matrices elementales en coordenadas globales se procede a ensamblar la matriz de rigidez global K y el vector de carga global F. La solución al problema (vector de desplazamientos global D) se calcula resolviendo el sistema de ecuaciones matricial definido por:
KD = F (9)
Las condiciones de borde consideradas son las siguientes:
Debido a que existe una relación de dependencia entre las fuerzas de contacto y las fuerzas de fricción generadas, se hace necesario definir un procedimiento iterativo, el cual se muestra a continuación:
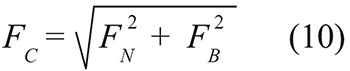
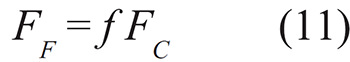
Se calcula el vector momento generado por el vector fuerza friccional a través de un producto vectorial, tomando en cuenta como brazo de palanca el radio externo del tubo.
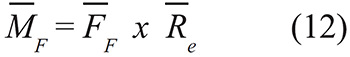
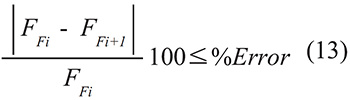
Es importante mencionar que
NFases = NElementos - 1.
La evaluación y validación de la metodología de cálculo desarrollada se realizó a través de su aplicación en diferentes casos de campo de los cuales mencionaremos dos de ellos, específicamente en el análisis post-operacional de dos pozos tipo J del campo Santa Rosa, distrito Anaco – estado Anzoátegui, Venezuela, el cual presentó problemas de pega de tubería o atascamientos. En dicho pozo se tomaron registros de carga en el gancho mientras se estaba realizando el proceso de colocación del revestidor en el hoyo (bajada de tubería).
El valor de carga en el gancho medido en el taladro viene a ser representado en el modelo numérico desarrollado por la reacción en dirección tangencial del primer nodo, o nodo ubicado en el inicio del pozo. Los valores de carga en el gancho medidos en operación son comparados con aquellos estimados a través del modelo y se podrá verificar si estos últimos representan o no una buena predicción a los valores reales.
Pozo 1. El primer caso a estudiar es un pozo tipo J con una sección tangente a 46° de inclinación y que alcanza una profundidad vertical de 10460 pies. En dicho pozo no se presentaron problemas durante la operación de bajada del revestidor de 7 pulgadas de diámetro externo y 35 lb/pie de peso. La operación se realizó utilizando una sarta de perforación de 5 pulgadas de diámetro externo y 19,5 lb/pie de peso.
El revestidor anterior tiene un diámetro interno de 8,535 pulgadas y fue colocado hasta una profundidad medida de 9395 pies (profundidad de la zapata).
En la Figura 3 se muestra una representación de la trayectoria del pozo en una vista en tres dimensiones, una vista de planta, y una proyección en un plano azimutal a 67°.
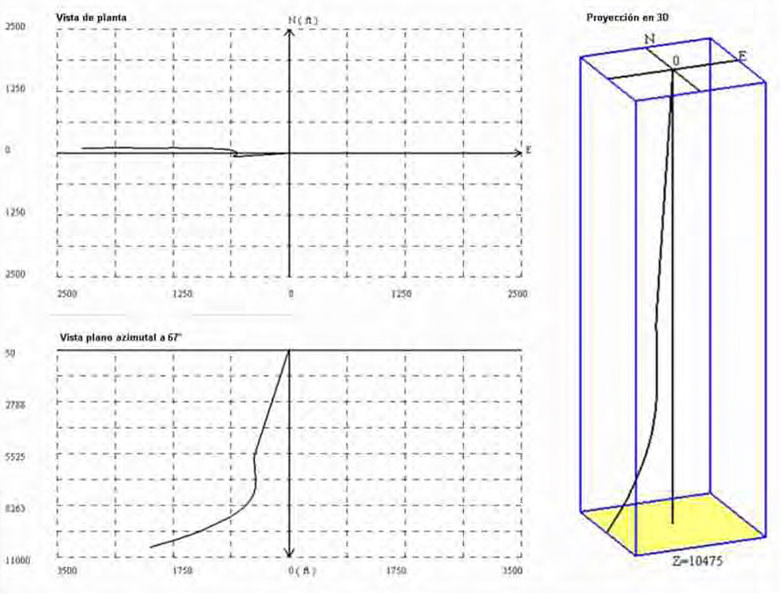
La operación se realizó utilizando un lodo de 9 lb/gal de densidad. El material del revestidor es acero con un módulo de elasticidad de 29,3x106 psi y un peso específico de 490 lb/pie3. El peso del bloque viajero fue de 45000 lb.
Para este pozo, se presenta el caso de una operación de bajada de liner o tubería colgada de producción, Dicha operación se realiza utilizando una sarta de perforación.
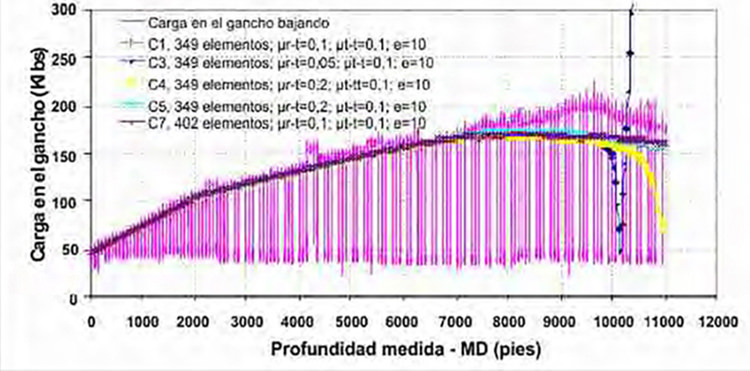
Para la primera discretización se tomaron elementos de 40 pies de longitud para el liner y 30 pies de longitud para la sarta de perforación (un elemento por cada tubo roscado), 297 elementos representando la sarta de perforación y 52 elementos la tubería de producción, para un total de 349 elementos en el modelo. Luego se realizó otra discretización tomando elementos de 20 pies de longitud, 105 elementos representando la tubería de producción y elementos de 30 pies de longitud, 297 elementos representando la tubería de producción, para un total de 402 elementos en el modelo.
Las corridas C1, C3 y C4 se realizaron colocando apoyos en todos los nodos, a diferencia de las corridas C5 y C7 que se realizó colocando un apoyo cada 2 nodos, entiéndase por apoyo a la restricción de movimiento transversal a la dirección de la trayectoria.
Luego de analizar los resultados se pudo notar que las estimaciones mostradas en las curvas C1, C5 y C7 son las que presentan mejor ajuste con respecto a los resultados obtenidos en campo, razón por la cual podemos inferir que para el modelo numérico desarrollado y en la zona estudiada los valores de coeficiente de fricción en la interfase tubo-roca (para los tubulares utilizados en el estudio) es de 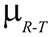
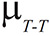
Una vez estimados los factores de fricción del campo Santa Rosa podemos utilizar dichos valores para los estudios de torque y arrastre de pozos vecinos.
Pozo 2. El segundo pozo en estudio es tipo J y finaliza con una sección tangente a 42° a los 9620 pies. Dicho pozo presentó eventos de pega de tubería durante la bajada del revestidor de 9 5/8 pulgadas de diámetro externo y 53 lb/pies de peso a aproximadamente 9000 pies de profundidad medida. El revestidor anterior tiene un diámetro interno de 12,4 pulgadas y fue colocado hasta una profundidad de 5676 pies (profundidad medida de la zapata).
En la Figura 5 se muestra una representación de la trayectoria del pozo en una vista en tres dimensiones, una vista de planta, y una proyección en un plano azimutal a 59°.
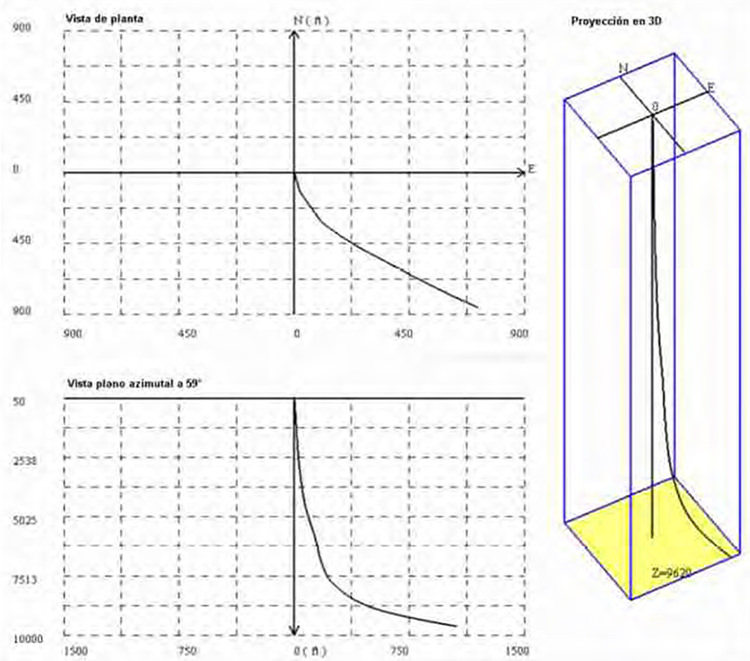
Dicha operación se realizó utilizando un lodo de 10,5 lb/gal de densidad. El material del revestidor es acero con un módulo de elasticidad de 29,3x106 psi y un peso específico de 490 lb/pie3. El peso del bloque viajero fue de 62000 lb.
Utilizando los factores de fricción estimados, para la primera discretización se tomaron elementos de 40 pies de longitud, lo que equivale a un elemento por cada tubo roscado (247 elementos por todo el modelo) y se colocaron apoyos o restricciones de movimiento transversal a la dirección del pozo cada dos nodos (cada 80 pies).
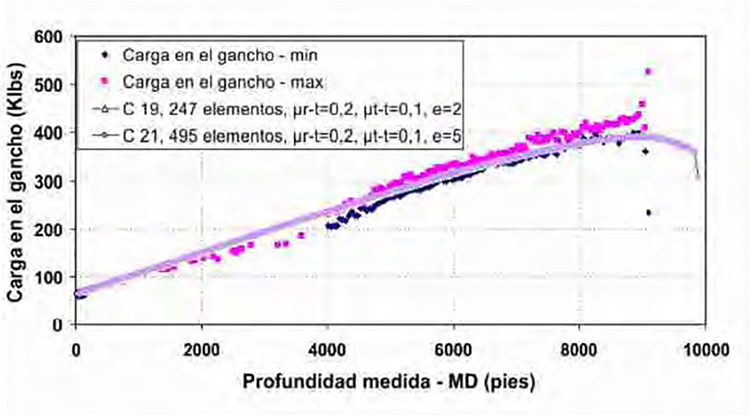
Para verificar que la discretización haya sido la correcta, se procedió a realizar una corrida adicional utilizando los valores de coeficientes de roce estimados, un error máximo admitido de 5% y una longitud de elemento de 20 pies, lo que equivale a dos elementos por tubo roscado (495 elementos por todo el modelo), manteniendo los apoyos cada dos nodos (cada 40 pies). En la Figura 7 se presentan los resultados obtenidos en esta corrida en comparación con los obtenidos en la corrida 19 y las mediciones reales.
En la Figura 6 se puede notar que los resultados de la simulación utilizando 247 elementos se superpone a los resultados obtenidos en la simulación utilizando 495 elementos, lo que lleva a concluir que ambas discretizaciones generan resultados confiables, o dicho de otra forma que se está en la zona asintótica de la curva de convergencia de malla usualmente utilizada razón por la cual los resultados siguen siendo muy similares aún al aumentar al doble el número de elementos utilizados.
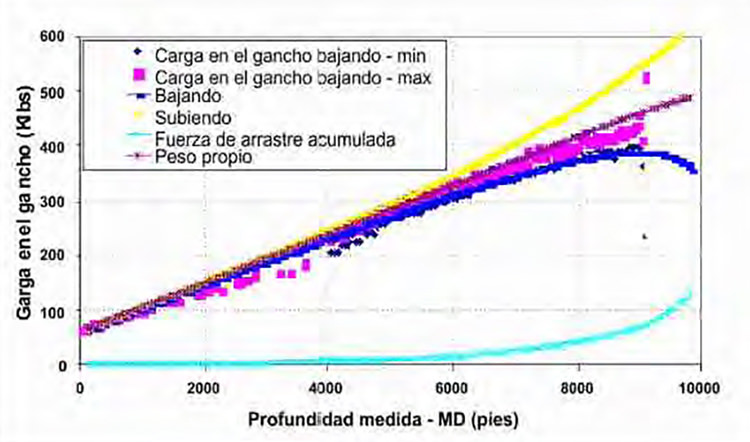
En la Figura 7 se muestran las gráficas de peso en el gancho bajando tubería (SOW), peso en el gancho subiendo tubería (PUW), peso en el gancho sin torque y arrastre (ROB) y la fuerza de arrastre acumulada a través de la simulación utilizando los datos estimados (247 elementos). Dichos resultados concuerdan con las estimaciones teóricas en la cuales se menciona que la fuerza en el gancho será mayor en operaciones de subida de tubería y será menor en operaciones de bajada de tubería, y por supuesto la fuerza de arrastre acumulada tiene un comportamiento creciente en función de la profundidad medida en el pozo.
Entre los parámetros a estimar en un estudio de torque y arrastre se tiene la fuerza lateral o fuerza de contacto entre el revestidor y las paredes del hoyo o del revestidor anterior, ya que se recomienda mantener la fuerza lateral en las juntas por debajo de 2000 lbs cuando se usa lodo base agua y por debajo de 3000 lbs al usar un lodo base aceite, con la finalidad de reducir el desgaste en las juntas de tubería y en los revestidores, y prevenir el agrietamiento por calor (fisuras que se forman en el acero por fatiga térmica – heat checking). Con la finalidad de comparar el desarrollo de la fuerza lateral bajando tubería con la curva de severidad de la pata de perro, y adicionalmente, evaluar la influencia que tiene sobre dicha fuerza el espaciamiento entre centralizadores, en la Figura 8 se muestran las estimaciones de fuerza lateral para las corridas bajando tubería utilizando 247 elementos y colocando apoyos cada 2 elementos (un apoyo cada 80 pies), y utilizando 495 pies y colocando apoyos cada 2 elementos (un apoyo cada 40 pies) contrastándolas con la severidad de la pata de perro (Dog Leg Severity).
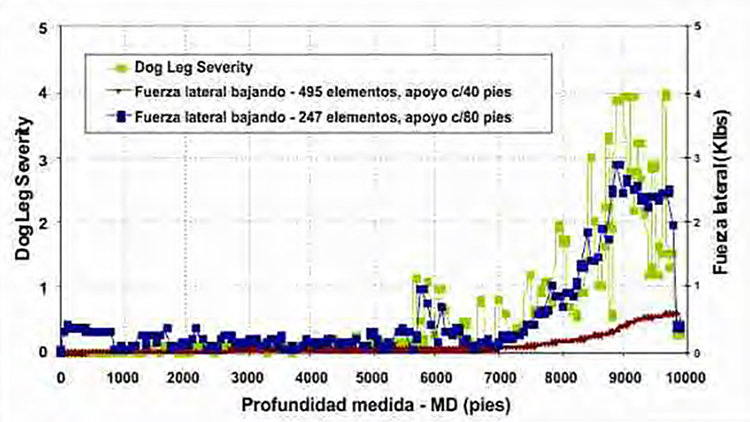
De la figura anterior se puede notar que a medida que aumenta la severidad de la pata de perro, las estimaciones de fuerza lateral también van en incremento, esto se debe a que desvíos acentuados y severos en el pozo pueden incrementar las fuerzas de contacto entre la tubería y las paredes del hoyo o del revestidor anterior. También se nota que a medida que aumenta el número de apoyos la fuerza lateral en cada uno de ellos disminuye, esto se debe a que el peso de las tuberías se distribuye en más puntos.
A lo largo de las últimas dos décadas, motivado por el aumento de la demanda mundial de hidrocarburos, se ha incrementado la construcción de pozos altamente inclinados, de alcance extendido, incluyendo pozos horizontales, que incorporan la producción a través de revestidores cementados y camisas de producción. En estos casos, la colocación óptima de los centralizadores se logra mediante el equilibrio entre un alto “standoff” y un bajo arrastre.
En la Figura 9 se muestra el “standoff” estimado a partir de los desplazamientos transversales calculados en los nodos no apoyados. En dicha figura podemos notar como el uso de centralizadores (rígidos en este caso), puede ayudar a alcanzar una correcta centralización, como el simple hecho de disminuir la distancia entre centralizadores mejora drásticamente el “standoff”.
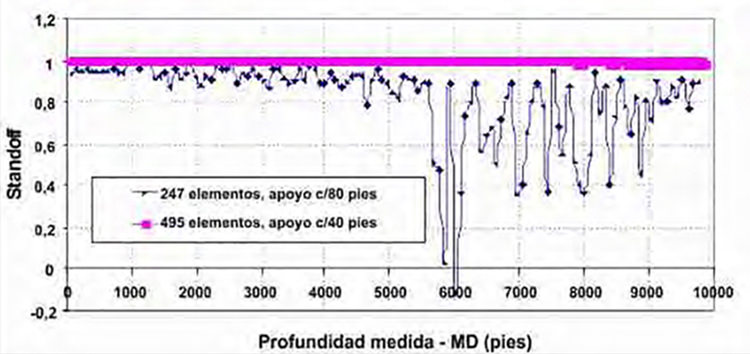
También se puede notar en la figura que la disminución importante en el standoff (por debajo de 0,8) ocurre justo en la zona donde tenemos un incremento importante en los valores de Dog Leg Severity. Vale la pena destacar que la distribución de apoyos (centralizadores rígidos) en el modelo a través de la herramienta desarrollada se realizó de forma uniforme, en otras palabras, los centralizadores están distribuidos uniformemente. En la realidad la distribución de centralizadores debe realizarse tomando en cuenta la distribución de la severidad de la pata de perro calculada para todo el pozo y colocar los centralizadores en las zonas críticas, por ejemplo en la sección vertical del pozo no se van a necesitar tantos centralizadores como en la zona de construcción de ángulo.
Los principales aportes que se obtuvieron de esta investigación sobre el modelado numérico del fenómeno de torque y arrastre por el método del elemento finito se resumen a continuación: